Divide f2, the coefficient of the x term, by 2 to get \frac{f}{2}1 Then add the square of \frac{f}{2}1 to both sides of the equation This step makes the left hand side ofDomainall real numbers b2x^3x^23x;Let f (x) be polynominal of degree 3 such that f (3) = 1, f ′ (3) = − 1, f ′ ′ (3) = 0 and f ′ ′ ′ (3) = 1 2, then the value of f ′ (1) = is Hard View solution

Is Function Of F X X 2 1 X 1 Continuous At X 1 Quora
Let f(x 1/x)=x^2 1/x^2 then f(x) is
Let f(x 1/x)=x^2 1/x^2 then f(x) is-Given a function g with this property, we can easily construct a suitable f Just let f ( x) = { g ( x) x ≥ 0 g ( − x) x < 0 If g is additionally continuous then so is f We can find a lot of continuous g Pick a 1 ∈ ( 0, 1), let a 0 = 0 and recursively a n = a n − 2 2 1 for n ≥ 2Click here👆to get an answer to your question ️ Let f = { (x, x^21 x^2 )x∈ R } be a function from R into R Determine the range of f




Mc Ex 1 4 Unit 4 Formulae Polynomials And Algebraic Fractions
Let f(x)=x^23x1 and g(x)=x^34x^21 Find (fg)(x) A (fg)(x)=x^33x^23x B (fg)(x)=x^3 Get the answers you need, now! color (blue) (f (x)=5x1), so wherever we see an x, we input color (red) (g (x)=x^21) Doing this, we get color (blue) (5 (color (red) (x^21))1 Let's distribute the 5 to both terms to get 5x^251 Which can obviously be simplified to f (g (x))=5x^26 Recall that we want to know f (g (1)), and we know f (g (x)) now, so now we can plugX Well begun is half done You have joined No matter what your level You can score higher Check your inbox for more details {{navliveTestEngineeringCount}} Students Enrolled {{navliveTestMedicalCount}} Students Enrolled Start Practicing
Problem 1 Let a>0 be a known constant, and let θ>0 be a parameter Suppose X1,X2,,X n is a sample from a population with one of the following densities (a) The beta, θ2x2Thenwecanpluginfory to get f(x,y)=f(x)= ±x p 2x2 The boundary's critical points are precisely those values of x for which 0=f0(x)=⌥ 2(x2 1) p 2x2 This is only true when x = ±1 We then find the corresponding values of y and find the extreme points on the boundary are (1,1),(1,1),(1,1), and (1,1) • Alternatively, we couldLet f(x) = 2x – 1, g(x) = 3x, and h(x) = x^2 1 Compute the following 1 f(g(3)) 2 f(h(7)) Log On Algebra Rational Functions, analyzing and graphing Section Solvers Solvers Lessons Lessons Answers archive Answers Click here to see ALL problems on Rationalfunctions
1 If 2x 2y = 2x y, then dy dx is 2 The probability of solving a problem by three persons A, B and C independently is 1 2, 1 4 and 1 3 respectively Then the probability of the problem is solved by any two of them is 3 If f (x) = sin − 1 ( 2x 1 x2), then f' (√3) is 4Answer to 13 Let f(x)= 1 ;05xs1 0;1Graph f(x)=(x1)^22 Find the properties of the given parabola Tap for more steps Use the vertex form, , to determine the values of , , and Since the value of is positive, the parabola opens up Opens Up Find the vertex Find , the distance from the vertex to the focus



Let A R 2 B R 1 If F A B Is A Function Defined By F X X 1 X 2 Show That F Is One One Onto Sarthaks Econnect Largest Online Education Community




Let F X Be A Polynomial Function If F X Is Divided By X 1 X 1 X 2 Then Reminders Are 5 3 And 2 Respectively When F X Is Divided
Let F (X) =`{ (1 X, 0≤ X ≤ 2) , (3 x , 2 < X ≤ 3)}` Find FofProposition In general if E(X i) are finite for all i=1,n, then E(X 1 KX n)=E(X 1)KE(X n) Proof Use the example above and prove by induction Let X 1, X n be independent and identically distributed random variables having distribution function F X and expected value µ Such a sequence of random variables is Transcript Misc 6 Let f = {("x, " 𝑥2/(1𝑥2)) x ∈ R } be a function from R into R Determine the range of f f = { ("x , " 𝑥2/(1𝑥2)) x ∈ R } We find different values of 𝑥2/(1 𝑥2) for different values of x Domain Value will always be between 0 & 1 We note that Value of range y = 𝑥2/(1 𝑥2) is always positive Also, it is always between 0 and 1 Hence, Range is
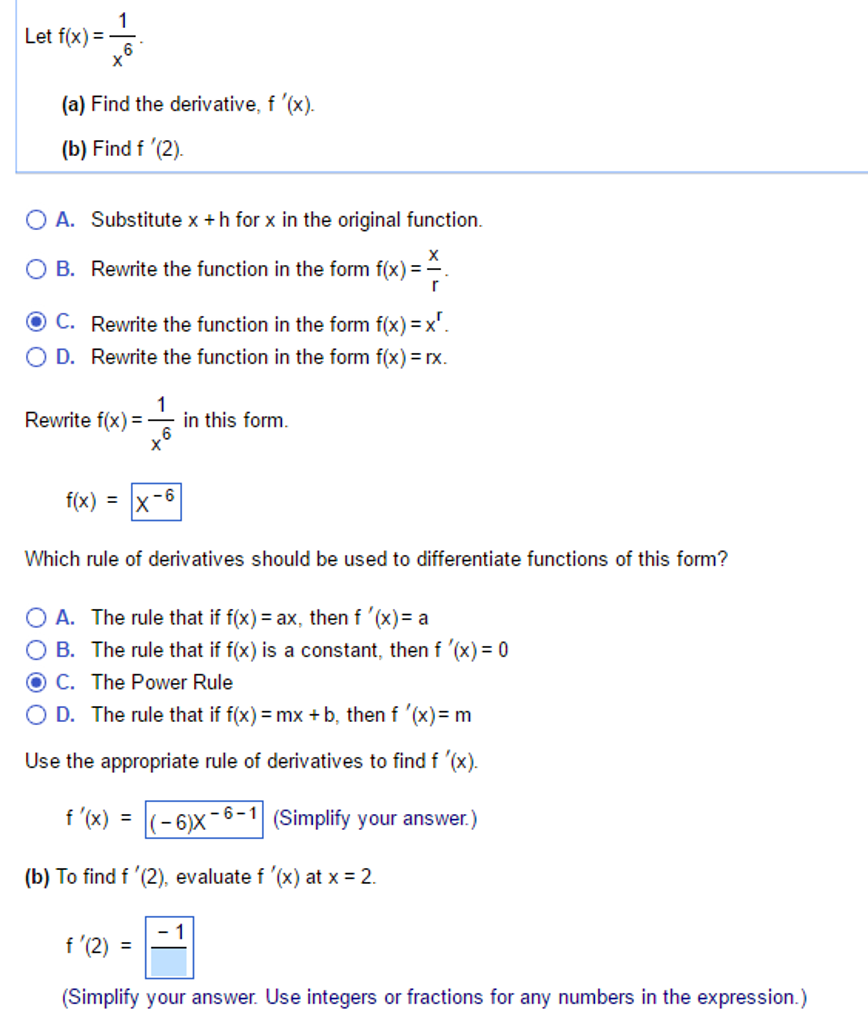



Let F X 1 X 6 Find The Derivative F X Find Chegg Com



Efisd Net Common Pages Displayfile Aspx Itemid
Let f(x) = x/(1 xn)1/n for n ≥ 2 and Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to Let's use our original identity, that f(g(x))=x, for all x f(g(1))=1 g^3(1)e^(g(1)/2) = 1 To make this equality simpler to look at, let u = g(1) u^3 e^(u/2) = 1 Well, you might be able to see that u=0 is a solution of this equation1 6= L 2, then lim (x,y)→(x0,y0) f (x,y) does not exist Remark When side limits do not agree, the limit does not exist Twopath test for the nonexistence of limits Remark When side limits do not agree, the limit does not exist C 0 C 1 2 y f ( x ) x x 2 x y 1 z f ( x, y) C 1 C 3 C Twopath test for the nonexistence of limits



Www3 Nd Edu Apilking Math Work Old exams Exams s13 M final sp13 solution Pdf
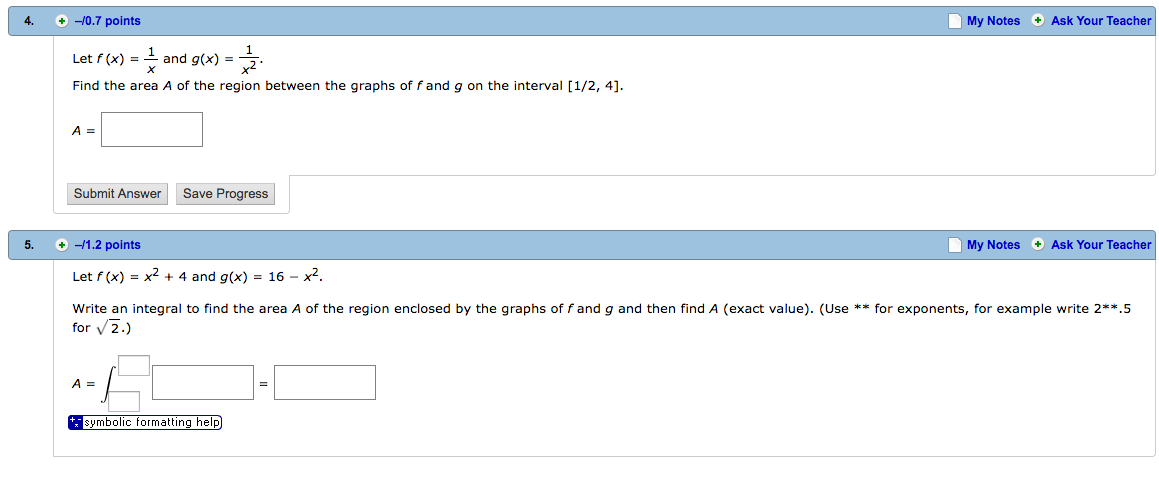



Let F X 1 X And G X 1 X 2 Find The Area A Of Chegg Com
Let f(x) = cos(x),x 0 = 02,x 1 = 03 Then fx 0,x 1 = cos(03)−cos(02) 03−02 =− (59) while f0 x 0 x 1 2 = −sin(025) =− so fx 0,x 1 is a very good approximation of this derivative 4 Interpolation Math 1070(x 1)(x 2) (x 2)2 After cancellation, we get lim x!2 (x 1)(x 2) (x 2)2 = lim x!2 (x 1) (x 2) Now this is a rational function where the numerator approaches 1 as x!2 and the denominator approaches 0 as x!2 Therefore lim x!2 (x 1) (x 2) does not exist We can analyze this limit a little further, by checking out the left and right hand limits at The random variables X and Y have the joint PMF pX,Y(x,y)={c⋅(xy)2,0,if x∈{1,2,4} and y∈{1,3},otherwise All answers in this problem should be numerical Find the value of the constant c c= Find P(Y How to get quick responses to your math questions Math is a wide subject, ranging from K to 11, college and university



Secure Media Collegeboard Org Digitalservices Pdf Ap Apcentral Ap15 Calculus Ab Q2 Pdf
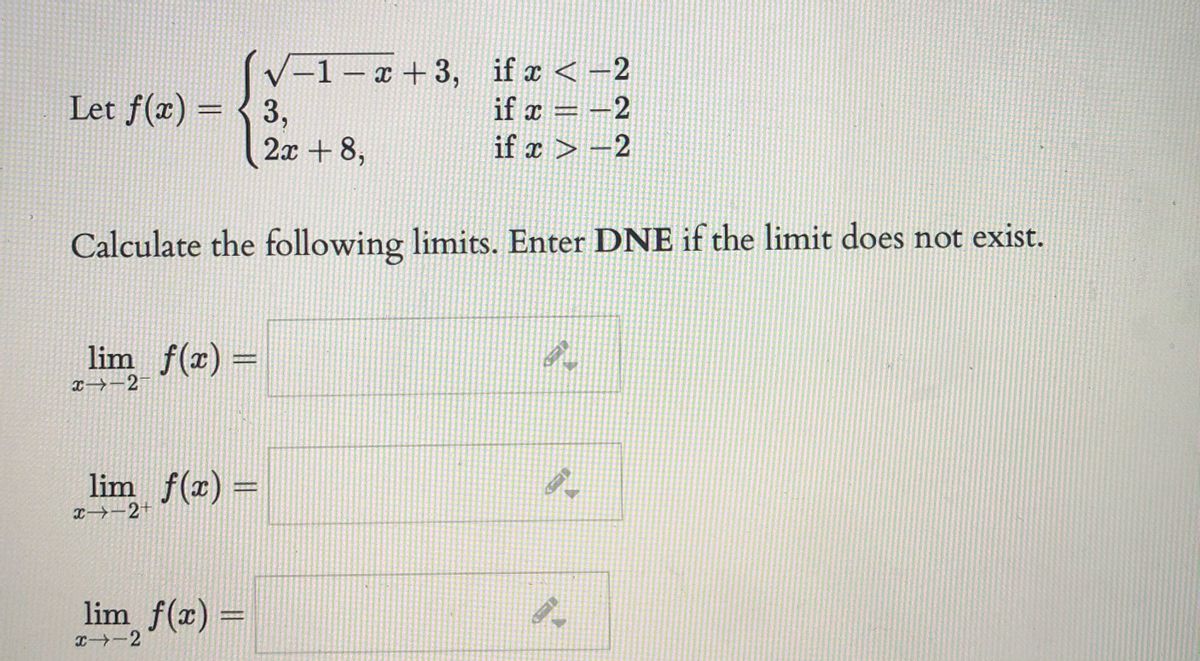



Answered 1 X 3 If X 2 If X 2 Let F X Bartleby
1 f X(y 1 n) where, f X() is the pdf of X which is given Here are some more examples Example 1 Suppose Xfollows the exponential distribution with = 1 If Y = p X nd the pdf of Y Example 2 Let X ˘N(0;1) If Y = eX nd the pdf of Y Note Y it is said to have a lognormal distribution Example 3 Let Xbe a continuous random variable with pdf f1 1=4 15=16 1=4 3=4 1=4 7=16 1=4 = 25=32 = L 4 is called the left endpoint approximation or the approximation using left endpoints (of the subin tervals) and 4 approximating rectangles We see in this case that L 4 = > A(becauseIt has been provided or mentioned that a function F(x1)=x^2–3x2 Interestingly, if we substitute a value of x1 in the place of x, we obtain, F((x1)1)=F(x) Therefore, F(x)=(x1)^2–3(x1)2=x^2–2x1–3x32=x^2–5x6 Hence, the function F(x) can



Solved Question 1 Let F X Sin 1 X 2 Then The Second Derivative At X 1 F 1 Equals A 2 3sqrt3 B 1 4sqrt3 C 2 Sqrt39 D Sqrt6 9 E Course Hero




Solving The Equation F X F 1 X Mathematics Stack Exchange
If f(x) = {((1 sinx)/(π 2x), x ≠ π/2), (λ, x = π/2) be continuous at x = π/2, then value of λ is asked in Limit, continuity and differentiability byDomain negative real numbers d2x^3xThen 1 0 etxf X(x)dx= Lf X( t) Use this moment generating function to compute the rst and second moments of X Exercise 132 Let Xbe a random ariablev whose probability density function is given by f X(x) = (e 2x 1 2 e x x>0 0 otherwise (a)Write down the moment generating function for X



Www3 Nd Edu Math Restricted Coursearchive 100level 126 f f Stanton Quizzes Exam1 Sol Pdf



Www Southhadleyschools Org Cms Lib Ma Centricity Domain 11 5 4 Pdf
A) f(x) = 2x1 Bijective This is injective because for every a 6= b, we have f(a) 6= f(b) (every number is 1 more than 2 times some number) We also know that the function is surjective because the range is all real numbers from 2((y 1)=2)1 = y b) f(x) = x2 1 Not injective and not surjective We know the function is not injective because weLet A=\left\ { x\in R1\le x\le 1 \right\} =B, then the mapping f Filo Class 12 Math Calculus Relations and Functions II 539 150 Let A = {x ∈ R −1 ≤ x ≤ 1} = B, then the mapping f A → B given by f (x) = x∣x∣ is injective but not surjectiveFind the Roots (Zeros) f(x)=2(x1)^22 Set equal to Solve for Tap for more steps Simplify Tap for more steps Simplify each term Tap for more steps Rewrite as Expand using the FOIL Method Tap for more steps Apply the distributive property Apply the distributive property Apply the distributive property



Secure Media Collegeboard Org Digitalservices Pdf Ap Apcentral Ap15 Calculus Ab Q2 Pdf



Let F X 1 X 0 X 2 F X 3 X 2 X 3 Determine The Form Of G X F F X And Hence Find
2 (a) Define uniform continuity on R for a function f R → R (b) Suppose that f,g R → R are uniformly continuous on R (i) Prove that f g is uniformly continuous on R (ii) Give an example to show that fg need not be uniformly continuous on R Solution • (a) A function f R → R is uniformly continuous if for every ϵ > 0 there exists δ > 0 such that f(x)−f(y) < ϵ for all xTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Let f(x)=x1x1Then f is differentiable in Ex 12, 10 Let A = R − {3} and B = R − {1} Consider the function f A → B defined by f (x) = ((x − 2)/(x − 3)) Is f oneone and onto?




Let F X Int X 2 1 X 2 1 Sqrt 1 X 2 Dx And F 0 0 Then F 1 Is




Let F X 1 X 0 X 2 3 X 2 Lt X Lt 3 Determine The Form Of Brainly In
Let f(x)=2x^2x3 and g(x)=x1 Perform the indicated operation then find the domain (f*g)(x) a2x^3x^24x3;Domain all real numbers c2x^3x^24x3;Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange




Let F X 1 X 2 If X 0 1 If X 0 Sin X X If X 0 Chegg Com
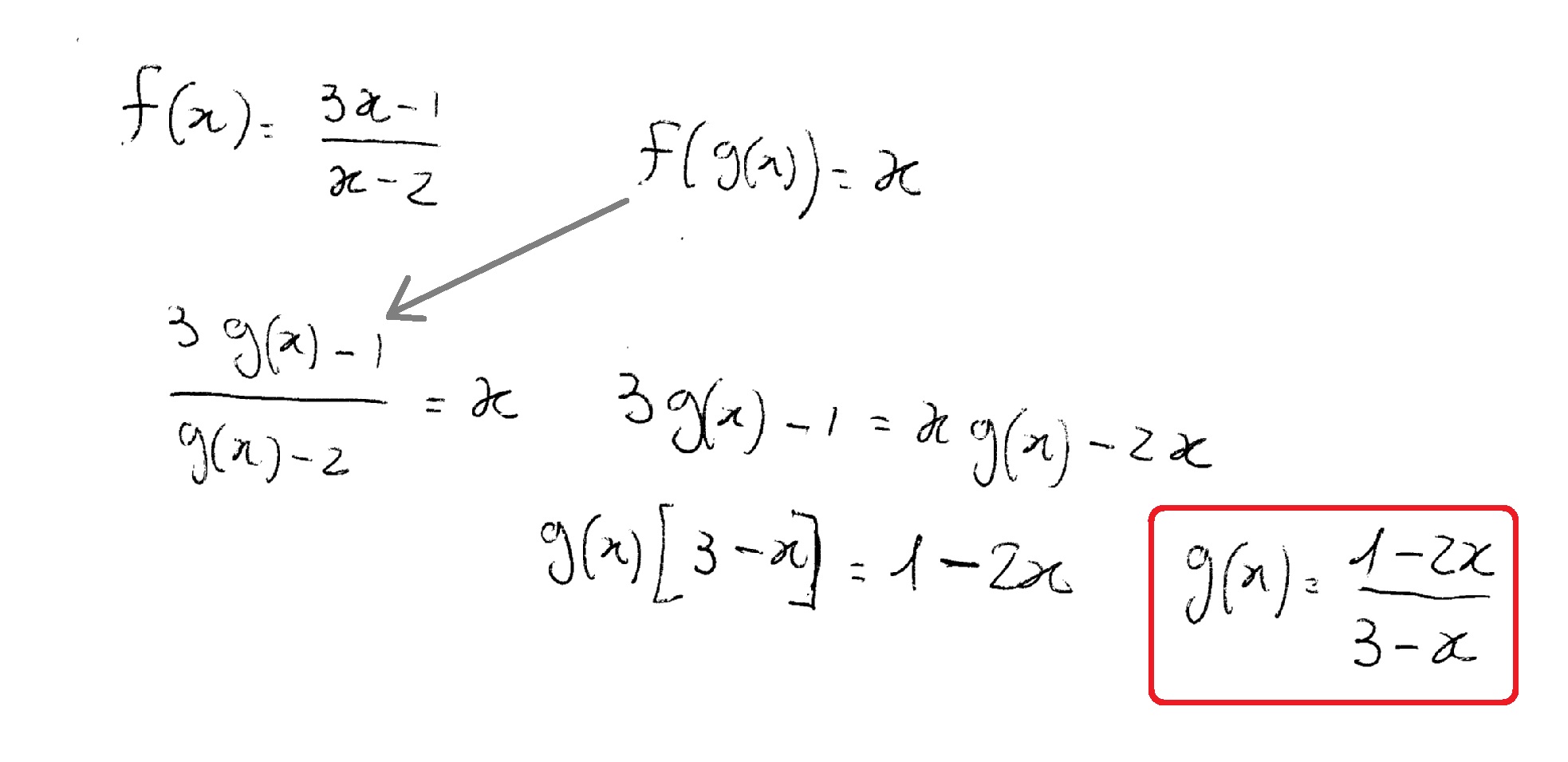



Let F X 3x 1 X 2 And F G X X How Do You Find G X Socratic
In some cases, we may need to do this by first computing lim x → a − f(x) and lim x → a f(x) If lim x → af(x) does not exist (that is, it is not a real number), then the function is not continuous at a and the problem is solved If lim x → af(x) exists, then continue to step 3 Compare f(a) and lim x → af(x) Get an answer for 'Let F(x)=f(f(x)) and G(x)=(F(x))^2 You also know that f(8)=4, f(4)=3, f'(4)=3, f'(8)=6 Find F'(8) and G'(8)' and find homework help for other Math questions atFor math0 \le x \le 1/math notice that mathf(x) \ge 0/math Also mathf(x)/math is quadratic with a negative coefficient for mathx^2/math so it has a




Let F X 1 X 0le Xle 2 And 3 X 2 Lt X Le 3 Find Fof X Youtube




What Is The Answer If F X 4x 7 Find F 1 X Quora
Let f(x) = x^2 6 and g(x) =(x8/x) Find (g ° f)(–7)Answer to Let f(x)=1x^2/3 Show that f(1) = f(1) but there is no number c in (1, 1) such that f'(c) = 0 Why does this not contradictSimple and best practice solution for F(x)=x^23x1 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it




Let F X X Root 1 X2 Show That Fofof X X Root 1 3x2 Brainly In




Let F X 1 X 0 Lt X Leq 2 And 3 X 2 Lt X Leq 3 Determine The Composite Function G X F F X Amp Hence Find The Point Of Discontinuity Of G If Any
Answer to Let f(x) = x^3x^2x1 \\ on \\ 1,2 find all numbers c satisfying the conclusion to the Mean Value Theorem By signing up, you'llTheorem 94C If P∞ k=1 uk = f uniformly on E, and if {uk} is continuous on E, then f is continuous on E Exnaple Let un(x)=x(1−xn), (0 ≤ x ≤ 1,n=0,1,2,···), and let f(x)= 1, if 0Steps for Solving Linear Equation f ( x ) = 1 \frac { 2 } { x 1 } , s f ( x) = 1 − x 1 2 , s Multiply both sides of the equation by x1 Multiply both sides of the equation by x 1 fx\left (x1\right)=x12 f x ( x 1) = x 1 − 2 Use the distributive property to multiply fx by x1




Mc Ex 1 4 Unit 4 Formulae Polynomials And Algebraic Fractions




If The Function F X X 2 1 X 1 When X 1 K When X 1
Question Let f(x)=x^21 and g(x)=12x Find the indicated values f(g(1)) and g(f(1) I have 4 of these types of questions on my homework and have no idea how to solve them This is the first one so there is other equation to help! The graph of f has a horizontal asymptote at y=3, and a removable discontinuity at x=2 1) Given the above information, find the values of a and b (Show work) 2) Find limit as x approaches 2 of f(x) (Show work) 3) At what values of x does f have a discontinuity due to a vertical asymptote?1 Example 1 f(x) = x We'll find the derivative of the function f(x) = x1 To do this we will use the formula f (x) = lim f(x 0 0) Δx→0 Δx Graphically, we will be finding the slope of the tangent line at at an arbitrary point (x 0, 1 x 1 0) on the graph of y = x (The graph of y = x 1 is a hyperbola in the same way that the graph of



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q4 Pdf




Let F X 0 If X Lt 0 X If 0 X 1 2 X If 1 Chegg Com




Let F X Frac 3x 2 2x 1 X 1 What Are The Types Of Asymptotes Of F X What Are The Equations Of All The Asymptotes Of F X Study Com



Search Q Inverse Functions Tbm Isch




Misc 2 If F X X2 Find F 1 1 F 1 1 1 1 Chapter 2




Let F X X2 4x 1 Then 1 F X Gt 0 For All X 3 F X 2 1 When X Lt 4 2 Flx Gt 1 When Brainly In




Answered Let F X 1 2ln 1 X 1 X Compute The Bartleby



Http Maths Dur Ac Uk Dma0wjz B1 Anlec1 Pdf




Let F X Be A Polynomial Function If F X Is Divided By X 1 X 1 X 2 Then Remainders Are 5 3 And 2 Respectively When F X Is Divided By X 3 2 X 2 X




Sketch The Graph F X 1 X And 1 3 X Youtube




Let F X 1 X If X 1 X 2 If 1 Chegg Com




Let F X E X 1 X 2 And G X F X Then




Let F X 1 X 2 Find Each Of The Following Chegg Com




Is Function Of F X X 2 1 X 1 Continuous At X 1 Quora



Www Portnet Org Cms Lib6 Ny Centricity Domain 276 1st and 2nd derivative test 1 Pdf




Let F X X 2 1 X 1 X 2 2 X 2 X 3 Chegg Com




Let F G Be Two Real Functions Defined By F X X 1 And G X 9 X 2 Then Described Each Of The Following Functions F G




Let F X 2 X And G X 1 X Find The Following Chegg Com



2




Let F X Be A Function Defined By F X 3x X 2x X 0 0 X 0 Show That X 0f X Does Not Exist



Www Southhadleyschools Org Cms Lib Ma Centricity Domain 11 5 4 Pdf




Let F R R Be Given By F X X 2 3 Then F 1 Is Given By Sqrt X 3 B Sqrt X 3 C X Sqrt 3 D None Of These




Use The Figure Below To Calculate The Following A Let K X F X 1 Find K 2 B Let G X F 1 X Find G 5 Study Com




Let F X X 1 X 1 Then F Is Differentiable In Youtube




Ex 1 3 6 Show F X X X 2 Is One One Find Inverse Of F



Examine The Differentiability Of F Where F Is Defined By F X 1 X If X 2 5 X If X 2 At X 2 Studyrankersonline



12 6 Arc Length
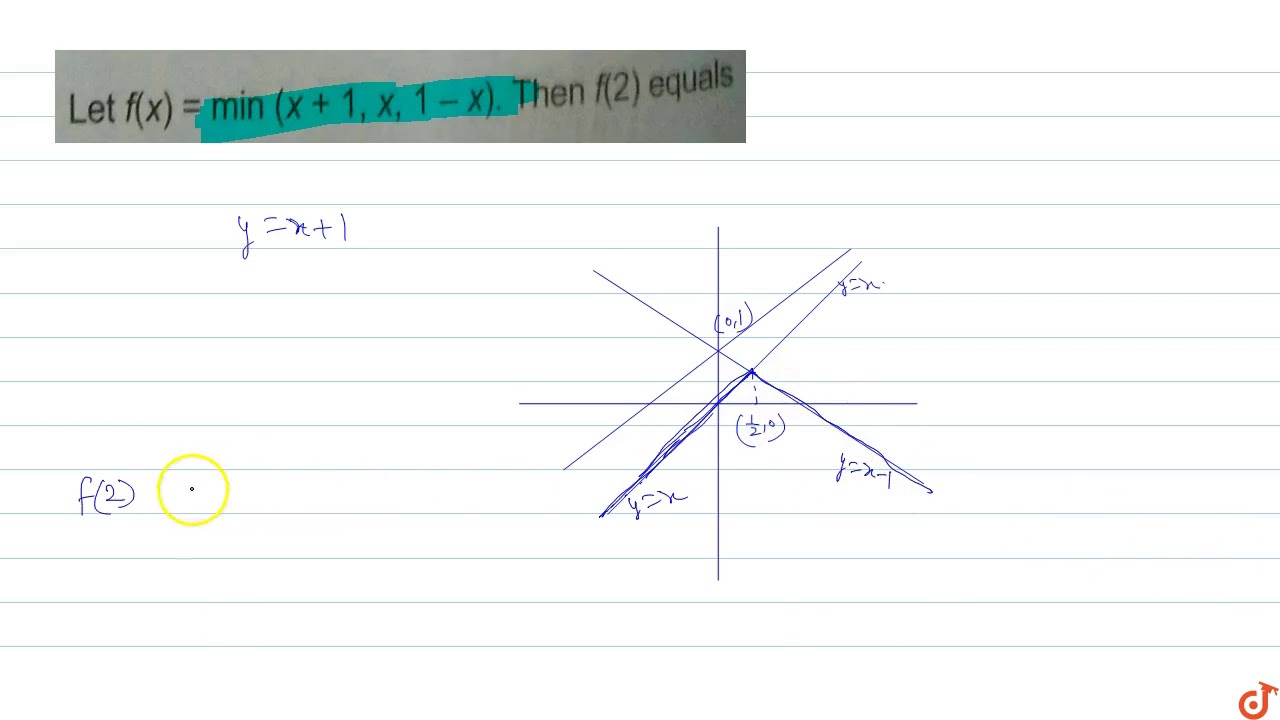



Let F X Min X 1 X 1 X Then F 2 Equals Youtube




Let F X 1 1 X 2 Then Range F




Let F X 2 10 X 1 And G X 3 10 X 1 If Fog X X Then X Is Equal To




If F X 0 For All X Then A F X F X For Every Chegg Com



Http Www Csus Edu Indiv B Binlu M130a Hw8sol Pdf




8 Let F X Log X Sqrt X 2 1 Then F Prime X Equals Begin Array Ll Text 1 Sqrt X 2 1 Text 2 Frac X Sqrt X 2 1 Text 3 1 Frac X Sqrt X 2 1 Text 4 Frac 1 Sqrt X 2 1 End Array



Find The Value Of A If The Function F X Defined By F X 2x 1 X 2 And A X 2 And X 1 X 2 Is



Secure Media Collegeboard Org Digitalservices Pdf Ap Apcentral Ap15 Calculus Ab Q2 Pdf



Www3 Nd Edu Apilking Math Work Old exams Exam 3f12 Sols Pdf




Let F X 1 X For X Ge 1 Ax 2 B For X 1 If F X Is Continuous And Differentiable At Any Point Then A A 1 2 B 3 2 B A 1 2 B 3 2 C A 1 B 1 D None Of These




Misc 6 Let F X X2 1 X2 X R Find Range Chapter 2




Let F X Root X 1 Root X 2 Then F 2 Is Equal To Brainly In




The Inverse Of F X Denoted F 1 X Is The Function That Reverses The Effect Of F X Ppt Video Online Download
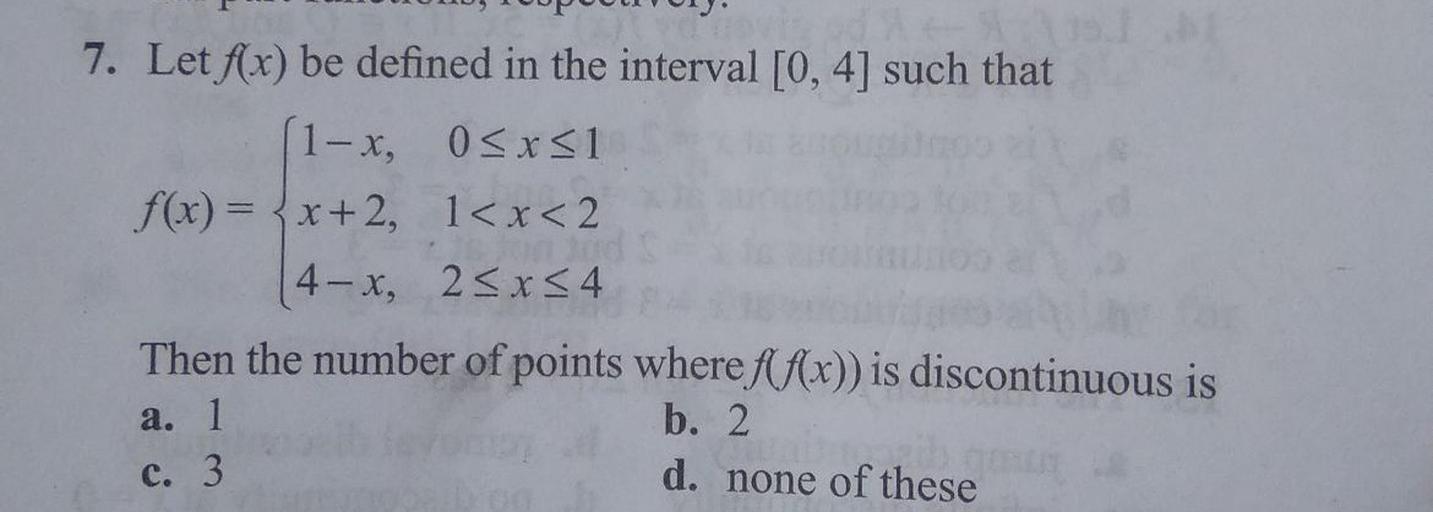



7 Let F X Be Defined In The Interval 0 4 Such That Math




Sample Exam 1




Let F X X2 2 If X Lt 1 X 2 2 If X Chegg Com



Solutions Manual For College Algebra 10th Edition By Larson Ibsn 9781




Let F X 2x Tan 1 X Ln X Sqrt 1 X 2 X In R Then




Let F X 1 X 1 And G X 1 X 2 X Notequalto Chegg Com




Let F X 1 X X 2 1 X 2 Find The Remainderoxwhen Fx Is Divided By 2x 1 Youtube



Q Tbn And9gcqj529kunx E23asbmwgf8sdjnucswezuevva8edino5czgfbjv Usqp Cau




1 Let Fx 2xa2 X 1 Evaluate O C 2 0 0 1 Chegg Com



View Question If F X X 2 1 X Find F 1



Let F X X 2 1 X 2 And G X X 1 X X R 1 0 1 If H X F X G X Then The Local Minimum Value Of H X Is Sarthaks Econnect Largest Online Education Community



F X X 2 Graph
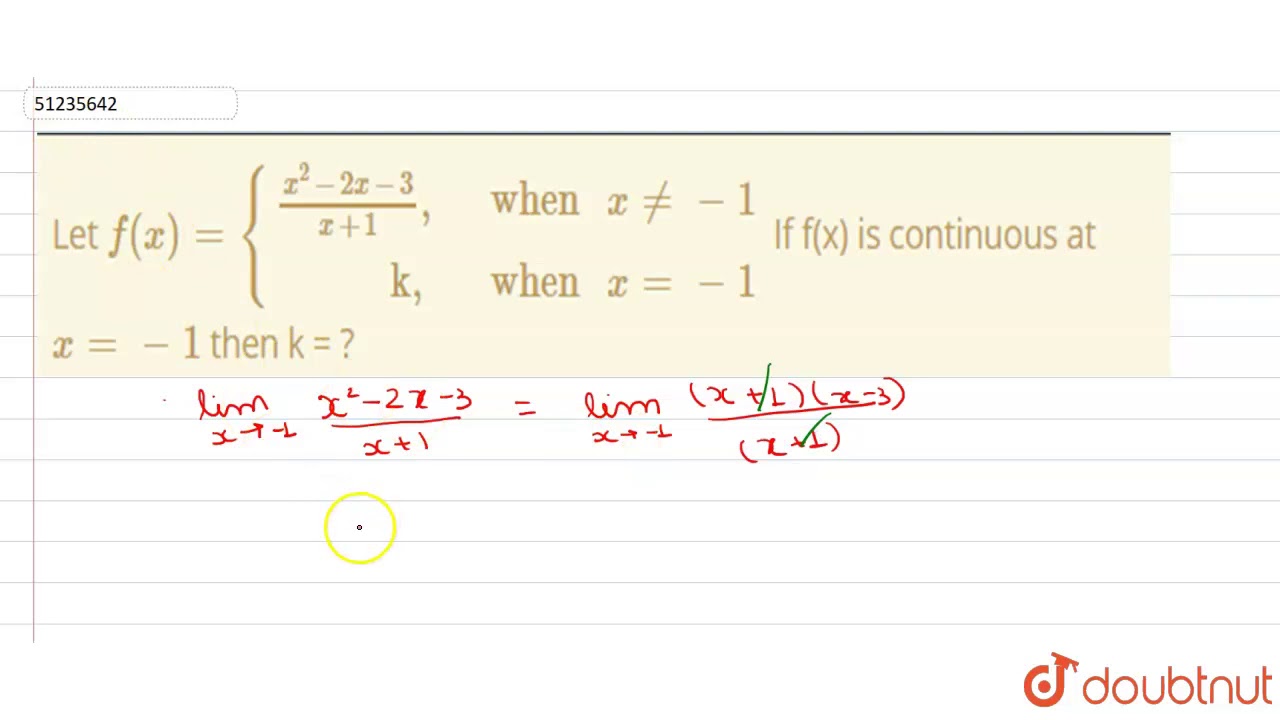



Let F X X 2 2x 3 X 1 When X 1 K When X 1 Youtube




Misc 2 If F X X2 Find F 1 1 F 1 1 1 1 Chapter 2



Q Tbn And9gctmiauoce Jgtrhnhoxjptyptyo5mw4r7aqizegy Baxprcttyz Usqp Cau



Www Stat Auckland Ac Nz Fewster 210 Notes 16s2 Ch4annotated Pdf




Misc 6 Let F X X2 1 X2 X R Find Range Chapter 2



Secure Media Collegeboard Org Digitalservices Pdf Ap Apcentral Ap15 Calculus Ab Q2 Pdf




Let F X 2x 3 X 3 If Function F One One And Onto Is F




Let F X 1 X 2 Use The Limit Definition Of The Chegg Com




Rd Sharma Solutions For Class 11 Maths Updated For 21 22 Chapter 3 Functions




Ex 1 3 6 Show F X X X 2 Is One One Find Inverse Of F




10 Let F X X2 X 1 Its Derivative Chegg Com




Section 2 7 One To One Functions And Their Inverses Pdf Free Download




Notes On Topics Of Algebra Notes



Www Ualberta Ca Rjia Math214 Hwks Sol9 Pdf




If The Function F R R Defined By F X 4 X4 X 2 Then Show That F 1 X 1 F X And Hence Deduce The Value Of F 14 2f 12 F 34
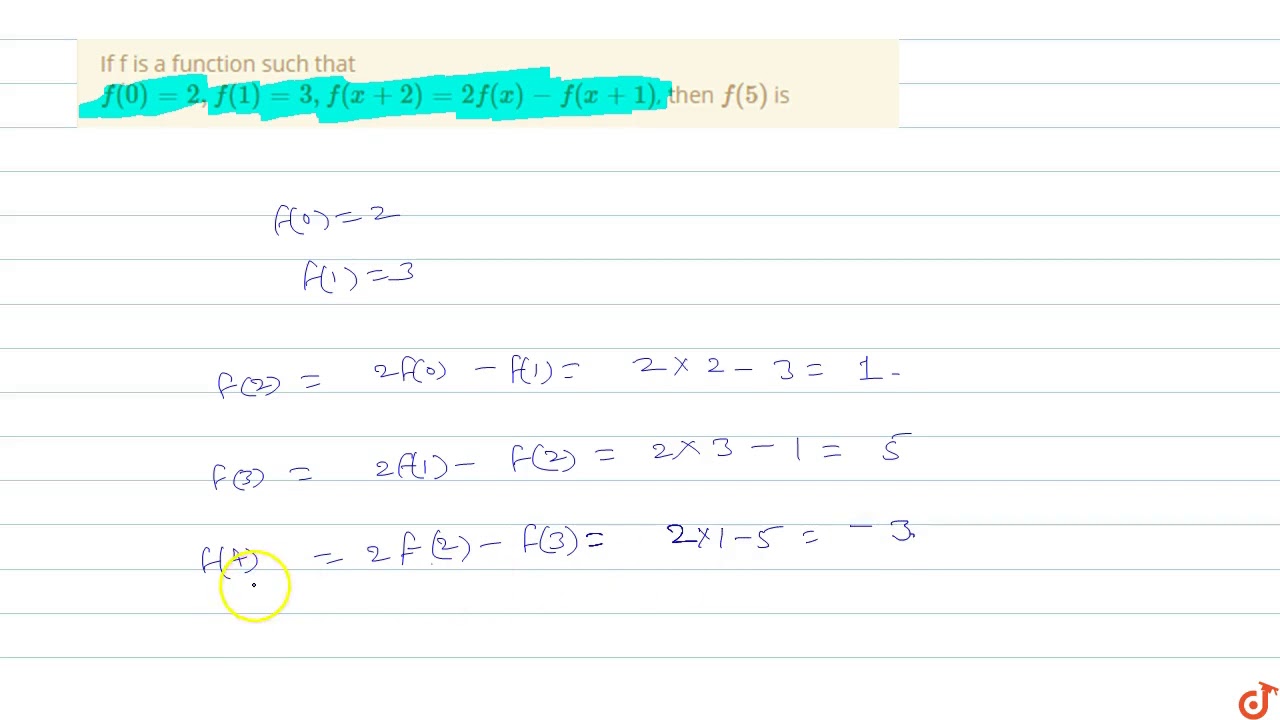



If F Is A Function Such That F 0 2 F 1 3 F X 2 2f X F X 1 Then F 5 Is Youtube



Courses Math Tufts Edu Math32 Exams Sol2 F07 Pdf



Secure Media Collegeboard Org Digitalservices Pdf Ap Apcentral Ap15 Calculus Q5 Pdf



Http Web Mnstate Edu Jamesju Fall11 Content M323exam3f11prackey Pdf




Let F X Log X Sqrt X 2 1 Then F X Equals Youtube



Let F X X 2 X 1 X 2 X 1 Then The Largest Value Of F X For X Belongs To The Interval 1 3 Is Iit Jee Main Advanced
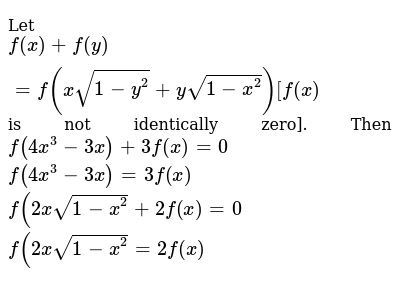



Let F X F Y F Xsqrt 1 Y 2 Ysqrt 1 X 2 F X Is Not Identically Zero Then F 4x 3 3x 3f X 0 F 4x 3 3x 3f X F 2xsqrt 1 X 2 2f X 0 F 2xsqrt 1 X 2 2f X
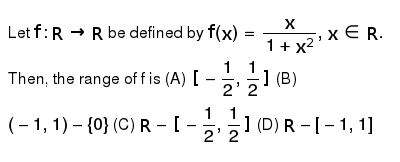



Let F R To R Be Defined By F X X 1 X 2 X In R Then The Range Of F Is A 1 2 1 2 B 1 1 0 C R 1 2 1 2 D R 1 1




1 Let A 2 3 And F X Xx 4x 7 Show That F A 0 Use This Result To Find aaa 1 2 Mathematics Topperlearning Com Dgp2odll




Let F X 1 X 0 X 2 3 X 2 Lt X 3 Then Find Fof Fof Means Brainly In




How To Solve This Question Integral E X X 2 1 X 1 2 Quora



If G X X If X 0 X 2 If 0 X 1 X 3 If X 1 How Do You Show That G Is Continuous On All Real S Socratic



How To Prove That F X X Sqrt X 2 1 Is Injective Quora



0 件のコメント:
コメントを投稿